最小二乗法とか
目次 |
目的
二つの値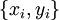 を沢山観測していると、どうやらこの値は直線にのるらしいことが分かった。
でも観測した値には誤差が含まれているので、どう頑張っても全部の点を通る直線を引くのは無理っぽい。
そこで、全ての観測した点に対してなるべく近くを通るような直線を求めるのを目指す。
を沢山観測していると、どうやらこの値は直線にのるらしいことが分かった。
でも観測した値には誤差が含まれているので、どう頑張っても全部の点を通る直線を引くのは無理っぽい。
そこで、全ての観測した点に対してなるべく近くを通るような直線を求めるのを目指す。
直線を求めるっていっても、紙に線を書くんじゃなくて、後で計算しやすいように直線の方程式の係数を求めるのがここのテーマ。
最小二乗法
またの名を最小自乗法。 読んで字のごとく誤差の2乗を最小にする係数を求める方法。
その1
以下の式を考える。
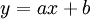
すると直線上の点は上式を満たすから、ある観測点の誤差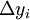 は次となる。
は次となる。
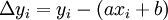
この値は正負両方の値をとるので2乗し、全ての観測点に対する和が最小になるように係数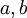 を定める。
を定める。
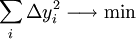
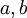 でそれぞれ偏微分して0とおき、連立させて解くと以下を得る。
でそれぞれ偏微分して0とおき、連立させて解くと以下を得る。
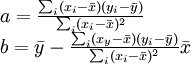
但し、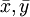 はそれぞれxとyの平均とする。
これを変形すると、
はそれぞれxとyの平均とする。
これを変形すると、
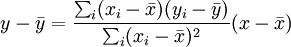
となるため、平均を通り、傾きが共分散/xの分散になる直線であることが分かる。
ちなみに行列を使って表すと、誤差ベクトル
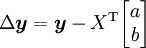
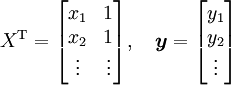
として、2乗誤差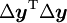 を係数ベクトルで微分すると次式を得る。
を係数ベクトルで微分すると次式を得る。
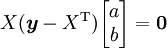
よって、
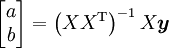
である。
その2
さて、勘のいい人は気付いていると思うけど、一つ目の方法はy軸の誤差しかみていないことが分かる。
ご丁寧にも とか書いてたしねぇ。
とか書いてたしねぇ。
普通に観測したデータはx軸にもy軸にも誤差が含まれるのが当然ってことで、次の式を考える。
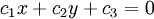
この式だと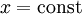 というy軸に平行な直線も表せるのと、両辺に0でない定数を掛けても同じ直線を表す(=定数倍の不定性がある)のに注意。
というy軸に平行な直線も表せるのと、両辺に0でない定数を掛けても同じ直線を表す(=定数倍の不定性がある)のに注意。
で、二乗の和を最小にする、と。
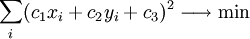
定数倍の不定性を除去するために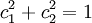 とすると、
とすると、
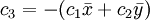
より、
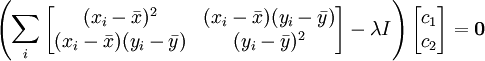
が得られ、求めるものは分散・共分散行列の最小固有値に対応する固有ベクトルだと分かる。
その1と同様に行列っぽく書くと、
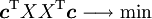
![X^\text{T} =
\begin{bmatrix}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
\vdots & \vdots & \vdots
\end{bmatrix}
, \quad
\boldsymbol{c} = [c1,\, c2,\, c3]^\text{T}](/wiki/images/math/7/7/d/77d64dff859b19d00880c99116e6bacb.png)
で、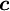 は
は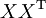 の最小固有値に対応する固有ベクトルになる。
但し、正規化の方法が若干違う(
の最小固有値に対応する固有ベクトルになる。
但し、正規化の方法が若干違う(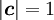 )ので注意。
)ので注意。
直線以外への当てはめ
当てはめに使っている方程式をぼーっと眺めてみると、
(係数1)(データ1) + (係数2)(データ2) + ・・・ = 0
という形をしている事が見えてくる。
つまり、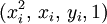 とすれば
とすれば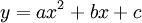 に当てはめたりできる。
に当てはめたりできる。
一般の2次曲線は

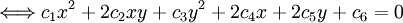
で表されるので
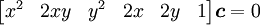
とすれば、楕円とか双曲線とか放物線とかに当てはめられる。 但し縮退する(2次の係数が0になるとか)場合があるので、計算できたからといっても安心できない。 それに誤差ののり方がそれぞれの要素で変わってくるため、当てはめの結果が最適であるという保証が無い点にも注意が必要。
